Phân phối Gamma là một trong những công cụ mạnh mẽ trong lĩnh vực phân tích chuỗi thời gian tài chính. Nó đặc biệt hữu ích khi phân tích các sự kiện xảy ra trong khoảng thời gian dài và có phân phối lệch. Trong bài viết này, chúng ta sẽ đi sâu vào các đặc điểm của phân phối Gamma, cách nó được sử dụng trong tài chính để mô hình hóa khối lượng giao dịch và rủi ro tín dụng, cũng như một ví dụ mô phỏng với Python để minh họa.

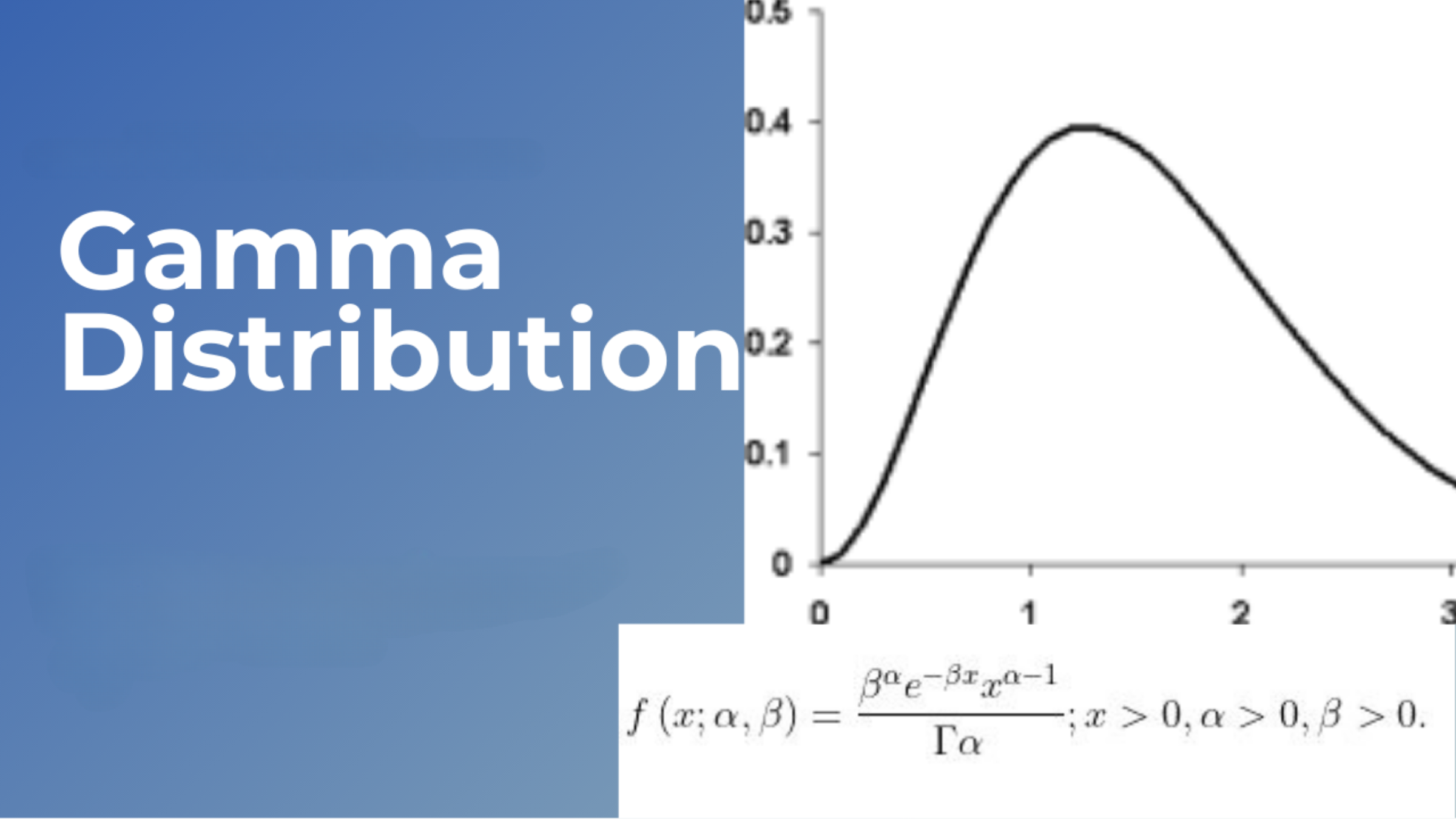
1. Đặc điểm của Phân phối Gamma

Phân phối Gamma được định nghĩa bởi hai tham số:

1. Tham số hình dạng (α): Quyết định hình dạng của phân phối.
2. Tham số tỷ lệ (β): Kiểm soát độ rộng hay phạm vi của phân phối.

Hàm mật độ xác suất cho phân phối Gamma được cho bởi công thức:

trong đó:

1. α (alpha) là tham số hình dạng.
2. β (beta) là tham số tỷ lệ.
3. Γ(α) là hàm Gamma, tổng quát hóa giai thừa cho các số thực và phức.

Phân phối Gamma có một số liên kết với các phân phối quan trọng khác:

1. Khi α = 1, phân phối Gamma trở thành phân phối mũ.
2. Với các giá trị nguyên của α, nó tương đương với phân phối Erlang.

2. Ứng dụng của Phân Phối Gamma

Phân phối Gamma được ứng dụng rộng rãi trong tài chính, đặc biệt là khi mô hình hóa các biến số không thể có giá trị âm và có phân phối lệch. Dưới đây là một số ứng dụng nổi bật:

1. Mô hình hóa khối lượng giao dịch

Trong chuỗi thời gian tài chính, phân phối Gamma thường được sử dụng để mô hình hóa khối lượng giao dịch hoặc thời gian chờ đợi giữa các sự kiện trên thị trường. Ví dụ, số lượng giao dịch trong một khoảng thời gian nhất định có thể không phân bố đồng đều – thường, khối lượng giao dịch cao hơn vào đầu hoặc cuối phiên giao dịch. Phân phối Gamma giúp mô tả sự biến đổi của khối lượng giao dịch một cách chính xác hơn.

1. Thời gian chờ tới lần vỡ nợ tiếp theo

Trong phân tích rủi ro tín dụng, phân phối Gamma hữu ích trong việc mô hình hóa thời gian cho đến khi xảy ra một sự kiện tín dụng (chẳng hạn như vỡ nợ). Không giống như phân phối mũ, phân phối Gamma có thể mô hình hóa các sự kiện trong đó rủi ro thay đổi theo thời gian, cung cấp một mô tả chính xác hơn về chu kỳ tín dụng.

1. Tính thanh khoản và lưu lượng đặt lệnh

Phân phối Gamma cũng được áp dụng để mô hình hóa khoảng thời gian giữa các lệnh thị trường liên tiếp, đặc biệt trong giao dịch tần suất cao, nơi các nhà giao dịch tham gia đặt lệnh mua và bán liên tục. Đặc tính lệch của phân phối Gamma giúp phản ánh sự biến động trong thời gian của các giao dịch này một cách hiệu quả.

3. Ví dụ: mô hình hóa khối lượng giao dịch

Giả sử chúng ta muốn mô hình hóa khối lượng giao dịch cho một cổ phiếu cụ thể trong giờ cao điểm giao dịch. Số lượng giao dịch trung bình mỗi giờ tuân theo phân phối Gamma với tham số hình dạng α = 3 và tham số tỷ lệ β = 1.

Với phân phối Gamma, chúng ta có thể trả lời các câu hỏi như:

1. Xác suất số lượng giao dịch vượt quá một ngưỡng nhất định là bao nhiêu?
2. Số lượng giao dịch kỳ vọng trong một khoảng thời gian nhất định là bao nhiêu?

4. Ví dụ với python: mô phỏng thời gian giao dịch theo phân phối gamma

Dưới đây là một ví dụ sử dụng Python để mô phỏng phân phối Gamma và minh họa các thời điểm giao dịch cho một cổ phiếu.

Giải thích:

1. Tham số α = 3 cho thấy phân phối có tính chất "thời gian chờ", với độ lệch vừa phải.
2. Biểu đồ cho thấy mật độ thời gian giữa các giao dịch, với hầu hết các giao dịch tập trung ở mức thời gian thấp hơn và có một đuôi dài chỉ ra các khoảng thời gian giao dịch thấp.

5. Ứng dụng trong Phân Tích Rủi Ro và Mô hình biến động

Trong quản lý rủi ro, phân phối Gamma được sử dụng để ước tính xác suất xảy ra các sự kiện hiếm gặp nhưng có tác động lớn, chẳng hạn như các giai đoạn thanh khoản cực đoan hoặc sự gia tăng đột ngột trong hoạt động giao dịch. Hiểu rõ về các sự kiện này là rất quan trọng để quản lý rủi ro, tối ưu hóa tiếp xúc và điều chỉnh chiến lược, đặc biệt trong các thị trường có biến động cao.

Ứng dụng trong giao dịch

Phân phối Gamma là công cụ quan trọng để mô hình hóa chuỗi thời gian tài chính có tính lệch như khối lượng giao dịch hoặc thời gian chờ đợi giữa các giao dịch.

Nó giúp các nhà giao dịch hiểu rõ hơn về tần suất của các sự kiện thị trường, cho phép quản lý thời gian thực hiện giao dịch và lưu lượng đặt lệnh hiệu quả hơn.

Các nhà quản lý rủi ro tận dụng mô hình Gamma để ước tính xác suất và tác động của các sự kiện hiếm gặp, cải thiện khả năng chịu đựng của danh mục đầu tư trong các giai đoạn căng thẳng.

Kết luận

Trên đây là cái nhìn tổng quan về vai trò của phân phối Gamma trong phân tích tài chính. Với việc áp dụng phân phối này, các nhà giao dịch và quản lý rủi ro có thể nắm bắt được hành vi của thị trường một cách linh hoạt hơn, từ đó xây dựng được các chiến lược giao dịch bền vững và hiệu quả.