[P2] Tổng hợp các phương pháp đánh giá rủi ro và hiệu suất trong đầu tư

22/04/2024

8,497 lượt đọc

Phần II - Tổng hợp các phương pháp đánh giá rủi ro và hiệu suất trong đầu tư 

Tiếp nối bài viết trong Phần 1 về 2 phương pháp đánh giá rủi ro và hiệu suất đầu tư là Sharpe và Sortino. Trong phần 2 này, QM Capital sẽ tập trung vào 3 phương pháp còn lại tỷ lệ Omega, tỷ lệ Calmar và tỷ lệ sụt giảm tối đa (Max Drawdown), mỗi công cụ đều có những ưu điểm riêng trong việc cung cấp cái nhìn sâu sắc về hiệu suất rủi ro và lợi nhuận của danh mục đầu tư. Những phương pháp này không chỉ giúp nhà đầu tư đánh giá bối cảnh hiện tại mà còn hỗ trợ dự đoán và chuẩn bị cho những biến động bất ngờ của thị trường. 

1. Tỷ lệ Omega

1.1. Giới thiệu về tỷ lệ Omega

Tỷ lệ Omega là một chỉ số đánh giá hiệu suất được sử dụng trong tài chính để đánh giá lợi nhuận điều chỉnh rủi ro của một khoản đầu tư. Tỷ lệ này tương tự như các chỉ số khác như Tỷ số Sharpe, nhưng đặt nhiều trọng tâm hơn vào phần đuôi của phân phối lợi nhuận.

Tỷ số Omega là tỷ lệ giữa lợi nhuận vượt qua một mức ngưỡng nhất định (thường là lợi nhuận tối thiểu chấp nhận (MAR)) so với tổng rủi ro ở phía dưới mức ngưỡng đó. Chỉ số này có thể cung cấp cái nhìn sâu sắc về hiệu suất điều chỉnh rủi ro của một danh mục đầu tư hoặc chiến lược đầu tư.

Một giá trị Tỷ số Omega cao nói chung chỉ ra một sự đánh đổi tốt giữa tiềm năng lợi nhuận và rủi ro của những tổn thất đáng kể. Ngược lại, một giá trị thấp cho thấy sự cân bằng lợi ích-rủi ro kém.

1.2. Ý nghĩa của tỷ lệ Omega 

Omega > 1: Cho thấy hiệu suất điều chỉnh rủi ro tốt. Danh mục đầu tư có khả năng cao đạt được lợi nhuận trên mức mục tiêu và khả năng thua lỗ đáng kể thấp.

Omega = 1: Giá trị ngưỡng phù hợp với lợi nhuận trung bình của khoản đầu tư. Danh mục có 50% khả năng đạt được lợi nhuận trên mức mục tiêu và 50% khả năng thua lỗ đáng kể.

Omega < 1: Cho thấy danh mục có khả năng thấp đạt được lợi nhuận trên mức mục tiêu và khả năng thua lỗ cao hơn, cho thấy hiệu suất điều chỉnh rủi ro kém.

Công thức của tỷ lệ Omega: 

OmegaRatio=Rp−MAR1n∑t=1nmax⁡[(MAR−rt),0]+1\text{OmegaRatio} = \frac{R_p - \text{MAR}}{\frac{1}{n} \sum_{t=1}^{n} \max{[(\text{MAR} - r_t ), 0]}} + 1

Trong đó: 

  1. Rp: Lợi nhuận kỳ vọng của tài sản hoặc danh mục đầu tư
  2. MAR: Lợi nhuận tối thiểu chấp nhận được
  3. rt: Lợi nhuận vào ngày t
  4. n: Độ dài kỳ hạn

1.3. Hạn chế của tỷ lệ Omega 

Tỷ lệ Omega là một công cụ có giá trị để đánh giá hiệu suất điều chỉnh rủi ro của danh mục hoặc chiến lược đầu tư, giống như bất kỳ các phương pháp nào để đo lường rủi ro và hiệu suất, Omega cũng có những hạn chế: 

Mức ngưỡng: Tỷ số Omega dựa trên một mức ngưỡng, thường được đặt tại mức lợi nhuận tối thiểu chấp nhận được (MAR) cho nhà đầu tư. Điều này có nghĩa là sự lựa chọn của mức ngưỡng có thể ảnh hưởng đến tỷ số, và các nhà đầu tư khác nhau có thể có các mức ngưỡng khác nhau, khiến việc so sánh hiệu suất của các danh mục hoặc chiến lược đầu tư khác nhau trở nên khó khăn.

Rủi ro đuôi: Tỷ số Omega là một biện pháp tốt để đo lường rủi ro đuôi, nhưng nó không xem xét các loại rủi ro khác, chẳng hạn như rủi ro lãi suất, rủi ro tiền tệ, rủi ro thanh khoản, v.v.

Nhạy cảm với ngoại lệ: Tỷ số Omega nhạy cảm với ngoại lệ, có nghĩa là tỷ lệ này bị ảnh hưởng đáng kể bởi các sự kiện cực đoan hoặc hiếm gặp. Điều này có thể khiến việc sử dụng tỷ số để so sánh hiệu suất của các danh mục hoặc chiến lược đầu tư khác nhau qua các giai đoạn khác nhau trở nên khó khăn.

Hạn chế bởi dữ liệu lịch sử: Việc tính toán tỷ số Omega dựa trên dữ liệu lịch sử, điều này có nghĩa là khả năng có sẵn và chất lượng của dữ liệu có thể ảnh hưởng đáng kể đến các giá trị được tính toán. Ngoài ra, dữ liệu lịch sử không thể được sử dụng để dự đoán hiệu suất tương lai của một khoản đầu tư.

1.4. Phân tích tỷ lệ Omega hàng năm của VOO Vanguard S&P 500 ETF bằng Python

import pandas as pd
import numpy as np
import yfinance as yf
import matplotlib.pyplot as plt

tickerSymbol = "VOO"
tickerData = yf.Ticker(tickerSymbol)
tickerDf = tickerData.history(period='1d', start='2010-1-1')
tickerDf['returns'] = tickerDf['Close'].pct_change()
MAR = 0 # Minimum Acceptable Return

# Omega Ratio calculation
omega_ratio = tickerDf['returns'].rolling(252).apply(lambda x: np.sum(x[x > MAR]) / np.sum(-x[x < MAR]))

# Aesthetics
plt.figure(figsize=(15, 7))
plt.style.use('seaborn-darkgrid')
palette = plt.get_cmap('Set1')

# Plot Omega Ratio
ax1 = plt.gca()
ax1.plot(omega_ratio.index, omega_ratio, color=palette(0), linewidth=1.5, label='Omega Ratio')

# Plotting a simple moving average of the omega ratio
ax1.plot(omega_ratio.index, omega_ratio.rolling(window=252).mean(), color='orange', linestyle='--', label='1-Year MA')

# Horizontal line for benchmark Omega Ratio of 1
ax1.axhline(y=1, color='red', linestyle='-.', label='Benchmark (1)')

# Shade region where Omega Ratio is above 1
ax1.fill_between(omega_ratio.index, omega_ratio, 1, where=(omega_ratio > 1), color='green', alpha=0.3,
                 label='Above Benchmark')

# Aesthetics for Omega Ratio
ax1.set_ylabel('Omega Ratio', fontsize=14, color=palette(0))
ax1.legend(loc='upper left')
ax1.set_title(f'Rolling 1-Year Omega Ratio with Stock Price (MAR: {MAR*100}%)', fontsize=16)

# Stock Price Plot on secondary y-axis
ax2 = ax1.twinx()
ax2.plot(tickerDf.index, tickerDf['Close'], color=palette(1), alpha=0.4, label='Stock Price')
ax2.set_ylabel('Stock Price', fontsize=14, color=palette(1))

plt.tight_layout()
plt.show()

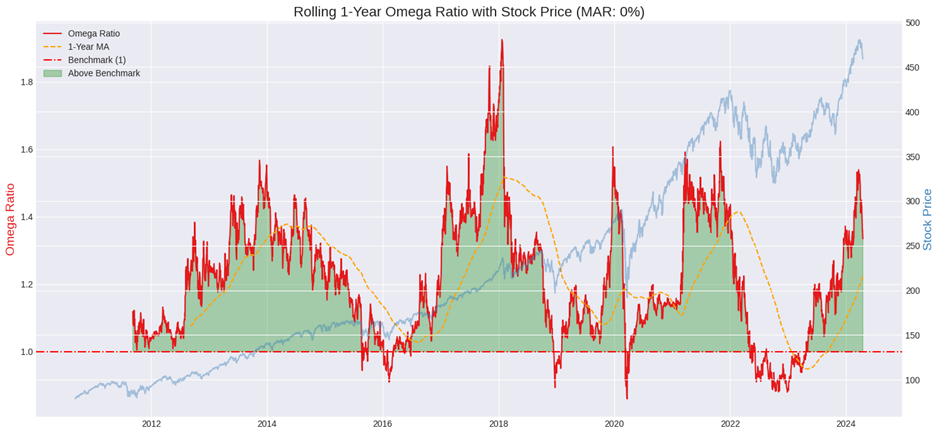
Ví dụ Phân tích tỷ lệ Omega hàng năm của VOO Vanguard S&P 500 ETF bằng Python

2. Tỷ lệ Calmar

2.1. Giới thiệu về tỷ lệ Calmar

Tỷ lệ Calmar là một chỉ số đo hiệu suất điều chỉnh theo rủi ro của một danh mục đầu tư. Được phát triển bởi Terry W. Young, người đặt tên theo California Managed Accounts Reports (CALMAR) vào năm 1990, tỷ lệ này đóng vai trò là thước đo hiệu suất mạnh mẽ. Điểm khác biệt chính giữa tỷ lệ Calmar và tỷ lệ Sharpe là tỷ lệ này được tính toán bằng cách sử dụng mức sụt giảm tối đa làm thước đo rủi ro.

2.2. Ý nghĩa của kết quả tỷ lệ Calmar:

Khi so sánh các quỹ đầu tư hoặc danh mục đầu tư với nhau, nhà đầu tư nên xem xét cả lợi nhuận của khoản đầu tư và các rủi ro liên quan đến nó. Và các quỹ cho thấy lợi nhuận cao hơn mà không phải chịu rủi ro lớn hơn được coi là các khoản đầu tư tốt hơn. Tỷ số Calmar được thiết kế để giúp hiểu liệu lợi nhuận cao hơn có liên quan đến rủi ro cao hơn hay không.

  1. Tỷ lệ Calmar âm có nghĩa là lãi suất không rủi ro cao hơn lợi nhuận của danh mục. Các giá trị dưới không không mang lại thông tin có ý nghĩa.
  2. Tỷ lệ Calmar từ 0 đến 1.0 cho thấy lợi nhuận của danh mục không vượt quá mức giảm giá tối đa trong một khoảng thời gian nhất định.
  3. Tỷ lệ Calmar trên 1.0 cho thấy lợi nhuận vượt nhẹ qua mức giảm giá. Khoản đầu tư này có thể được coi là rủi ro.
  4. Tỷ lệ Calmar trên 3.0 cho thấy lợi nhuận vượt trội so với mức giảm giá. Đây có thể là một chỉ báo của một khoản đầu tư ổn định.
  5. Tất cả các điều kiện khác ngang bằng, một quỹ hoặc danh mục đầu tư có tỷ số Calmar cao hơn là khoản đầu tư được ưu tiên.

Ví dụ: Giả sử giá trị của tỷ số Calmar cho một danh mục hoặc quỹ là 2, điều này có nghĩa là trong khoảng thời gian được chọn, lợi nhuận hàng năm vượt quá hai lần mức giảm giá tối đa.

Công thức:

Tỷ lệ Calmar = (Rp - Rf) /MD

Trong đó: 

  1. Rp: Lợi nhuận danh mục đầu tư hàng năm
  2. Rf: Lãi suất phi rủi ro hàng năm
  3. MD (Max Drawdown): Mức sụt giảm tối đa 

2.3. Hạn chế của tỷ lệ Calmar trong đầu tư

  1. Phụ thuộc vào khoảng thời gian phân tích: Tỷ số Calmar nhạy cảm với khoảng thời gian được chọn để phân tích, dẫn đến kết quả không nhất quán. Các khung thời gian khác nhau có thể mang lại các mức giảm tối đa khác nhau, ảnh hưởng đến tỷ số Calmar tổng thể.
  2. Nhạy cảm với các sự kiện ngoại lệ: Tỷ lệ Calmar rất dễ bị ảnh hưởng bởi mức giảm tối đa, có thể bị tác động đáng kể bởi các sự kiện cực đoan hoặc ngoại lệ. Điều này dẫn đến làm méo mó trong việc đánh giá hiệu suất điều chỉnh theo rủi ro.
  3. Gặp khó khăn trong việc so sánh giữa các lớp tài sản: Việc so sánh tỷ lệ Calmar giữa các lớp tài sản khác nhau sẽ gặp khó khăn do sự khác biệt giữa rủi ro - lợi nhuận và bản chất của các mức giảm. Điều quan trọng là nhà đầu tư cần xem xét bối cảnh và đặc điểm cụ thể của từng lớp tài sản khi sử dụng tỷ lệ Calmar cho việc so sánh.

2.4. Cách sử dụng tỷ lệ Calmar hiệu quả

Sử dụng nhiều phép đo hiệu suất: Để có được cái nhìn toàn diện về hiệu suất điều chỉnh theo rủi ro của khoản đầu tư, điều cần thiết là sử dụng nhiều phép đo hiệu suất. Tỷ lệ Calmar nên được sử dụng kết hợp với các phép đo hiệu suất điều chỉnh theo rủi ro khác, như Tỷ lệ Sharpe, Tỷ lệ Sortino, Tỷ lệ Treynor và Tỷ lệ Omega.

Xem xét khoảng thời gian đầu tư: Tỷ lệ Calmar sẽ cần xem xét đối với các khoản đầu tư có khoảng thời gian dài hơn, vì những biến động giá trị ngắn hạn có thể làm “méo” mức rút vốn tối đa.

Theo dõi và cập nhật thường xuyên: Nhà đầu tư nên thường xuyên theo dõi và cập nhật các tính toán Tỷ lệ Calmar để đảm bảo rằng nhà đầu tư đang đưa ra quyết định dựa trên dữ liệu mới nhất. Điều này đặc biệt quan trọng trong thời điểm thị trường biến động hoặc khi có những thay đổi đáng kể trong chiến lược đầu tư hoặc danh mục đầu tư.

2.5. Phân tích tỷ lệ Calmar hàng năm của VISA bằng Python

import pandas as pd
import numpy as np
import yfinance as yf
import matplotlib.pyplot as plt

tickerSymbol = "V"
tickerData = yf.Ticker(tickerSymbol)
tickerDf = tickerData.history(period='1d', start='2010-1-1')
tickerDf['returns'] = tickerDf['Close'].pct_change()

# Calmar Ratio calculation
calmar_ratio = tickerDf['returns'].rolling(252).apply(lambda x: (1 + x).cumprod()[-1] ** (252.0 / len(x)) / np.abs(x.min()))

# Threshold for Calmar Ratio
threshold_calmar = calmar_ratio.mean()

plt.figure(figsize=(15, 7))
plt.style.use('seaborn-darkgrid')
palette = plt.get_cmap('Set1')

ax1 = plt.gca()
ax1.plot(calmar_ratio.index, calmar_ratio, color=palette(0), linewidth=1.5, label='Calmar Ratio')
ax1.plot(calmar_ratio.index, calmar_ratio.rolling(window=252).mean(), color='orange', linestyle='--', label='1-Year MA')
ax1.axhline(y=threshold_calmar, color='red', linestyle='--', label=f'Threshold (Mean: {threshold_calmar:.2f})')
ax1.set_title('Rolling 1-Year Calmar Ratio with Stock Price', fontsize=16)
ax1.set_ylabel('Calmar Ratio', fontsize=14)
ax1.legend(loc='upper left')

ax2 = ax1.twinx()
ax2.plot(tickerDf.index, tickerDf['Close'], color=palette(1), alpha=0.4, label='Stock Price')
ax2.set_ylabel('Stock Price', fontsize=14)

plt.tight_layout()
plt.show()

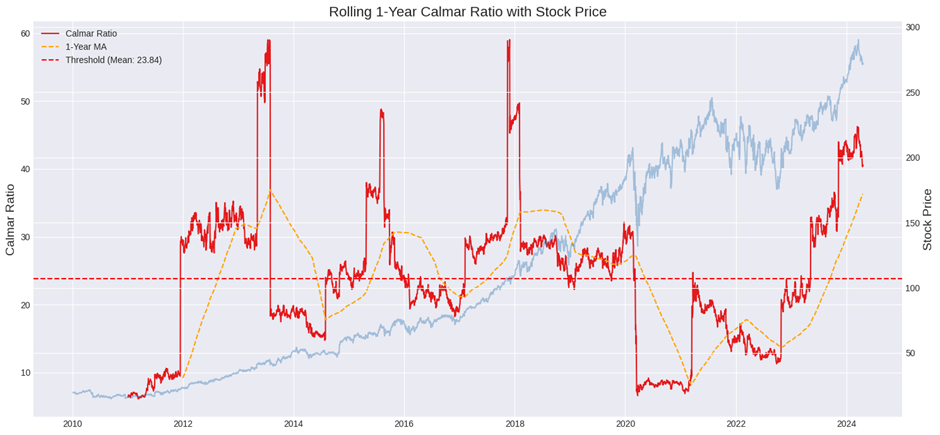
Ví dụ Phân tích tỷ lệ Calmar hàng năm của VISA bằng Python

3. Mức sụt giảm tối đa (Maximum Drawdown) 

3.1. Giới thiệu

Maximum Drawdown hay còn gọi là mức rút vốn tối đa là chỉ mức sụt giảm tối đa của tài khoản tính từ ở đỉnh vốn cao nhất đến phần đáy vốn thấp nhất tiếp theo sau đỉnh vốn đó. Maximum Drawdown của tài khoản giao dịch sẽ không được ghi nhận cho đến khi biến động vượt đỉnh, đáy thấp nhất.

Biểu đồ thể hiện Maximum Drawdown

Công thức 

Maximum Drawdown (%) = (Đáy vốn - Đỉnh vốn)/Đỉnh vốn×100%

Ví dụ cách tính Maximum Drawdown

Ví dụ cách tính Maximum Drawdown

3.2. Maximum Drawdown quan trọng như thế nào đối với các nhà đầu tư?

Đánh giá rủi ro: Mức rút vốn tối đa cung cấp cho nhà đầu tư thước đo rõ ràng về rủi ro giảm giá của một khoản đầu tư. Bằng cách hiểu được một khoản đầu tư có thể giảm giá trị bao nhiêu trong điều kiện thị trường không thuận lợi, nhà đầu tư có thể đánh giá mức độ rủi ro họ đang phải đối mặt và đưa ra các quyết định sáng suốt về quản lý danh mục đầu tư và phân bổ tài sản.

Đo lường biến động: Mức rút vốn tối đa có liên quan chặt chẽ với biến động, là một chỉ số đo lường sự thay đổi giá cả hay giá trị của một khoản đầu tư theo thời gian. Các sụt giảm giá lớn thường cho thấy biến động cao hơn. Nhà đầu tư nhạy cảm với biến động có thể sử dụng Max Drawdown như một phương tiện để đánh giá sự ổn định và khả năng dự đoán của một khoản đầu tư.

Quản lý rủi ro: Max Drawdown giúp nhà đầu tư thực hiện các chiến lược quản lý rủi ro để bảo vệ danh mục đầu tư khỏi những mất mát đáng kể. Bằng cách đặt ngưỡng chấp nhận sụt giảm giá trị được định trước, nhà đầu tư có thể thiết lập các lệnh dừng lỗ hoặc thực hiện các kỹ thuật phòng ngừa để hạn chế rủi ro giảm giá và bảo toàn vốn. 

3.3.Phân tích mức rút vốn tối đa (Max Drawdown) hàng năm của Coca-Cola bằng Python

import pandas as pd
import numpy as np
import yfinance as yf
import matplotlib.pyplot as plt

tickerSymbol = "KO"
tickerData = yf.Ticker(tickerSymbol)
tickerDf = tickerData.history(period='1d', start='2010-1-1')
tickerDf['returns'] = tickerDf['Close'].pct_change()

rolling_cumulative = (1 + tickerDf['returns']).cumprod()
rolling_max = rolling_cumulative.rolling(252, min_periods=1).max()
rolling_drawdown = (rolling_cumulative - rolling_max) / rolling_max

plt.figure(figsize=(15, 7))
ax1 = plt.gca()
ax1.plot(rolling_drawdown, label='Rolling Maximum Drawdown', linewidth=1.5, color='red')
ax1.set_title('Rolling 1-Year Maximum Drawdown with Stock Price', fontsize=16)
ax1.set_ylabel('Max Drawdown', fontsize=14)
ax1.legend()

ax2 = ax1.twinx()
ax2.plot(tickerDf['Close'], color='grey', alpha=0.3, label='Stock Price')
ax2.set_ylabel('Stock Price', fontsize=14)

plt.tight_layout()
plt.show()


📌 Link Google Colab: Tổng hợp các phương pháp đánh giá rủi ro và hiệu suất trong đầu tư


RiskMetrics Omega Ratio Calmar Ratio Maximum Drawdown
Chia sẻ bài viết

Đánh giá

(0)

0 Đánh giá

0 / 5

5

0

4

0

3

0

2

0

1

0
Hãy là người đầu tiên nhận xét bài viết này!

Đăng ký nhận tin

Nhập Email để nhận được bản tin mới nhất từ QM Capital.

Bài viết liên quan

Cách xây hệ thống giao dịch đa khung thời gian trên thị trường phái sinh VN30
19/10/2025
18 lượt đọc

Cách xây hệ thống giao dịch đa khung thời gian trên thị trường phái sinh VN30 C

Trong thị trường phái sinh Việt Nam, nơi thanh khoản tập trung gần như toàn bộ vào hợp đồng VN30F1M, hành vi giá thường nhiễu, dao động mạnh và chịu ảnh hưởng lớn từ dòng tiền ngắn hạn. Vì vậy, một hệ thống giao dịch chỉ dựa trên một khung thời gian duy nhất thường không đủ — bạn có thể đúng hướng nhưng vẫn lỗ chỉ vì vào sai nhịp.

Python và các thư viện cốt lõi trong xây dựng hệ thống giao dịch định lượng
18/10/2025
18 lượt đọc

Python và các thư viện cốt lõi trong xây dựng hệ thống giao dịch định lượng C

Python không chỉ là một ngôn ngữ lập trình phổ biến — trong lĩnh vực tài chính định lượng và giao dịch tự động (quant trading), nó đã trở thành công cụ chủ lực. Nhờ hàng loạt thư viện mạnh mẽ, lập trình viên và nhà đầu tư giờ có thể biến ý tưởng chiến lược thành mô hình thực thi — từ phân tích dữ liệu, backtesting tới triển khai live trading.

Khung thời gian trong giao dịch trong quant trading
16/10/2025
45 lượt đọc

Khung thời gian trong giao dịch trong quant trading C

Một trong những quyết định tưởng chừng đơn giản nhưng lại ảnh hưởng lớn nhất đến kết quả giao dịch — là việc chọn khung thời gian (time frame). Hầu hết các trader, đặc biệt là người mới, đều bắt đầu với câu hỏi: “Tôi nên giao dịch khung nào — 1 phút, 5 phút, hay khung ngày?” Thực tế, không có “khung thời gian tốt nhất”. Thị trường không quan tâm bạn vào lệnh ở 9h30 hay nắm giữ đến tháng sau. Cái thị trường phản hồi chỉ là xác suất và hành vi giá trong khung mà bạn chọn.

10 trader để đời: những góc nhìn chưa bao giờ cũ về thị trường
14/10/2025
57 lượt đọc

10 trader để đời: những góc nhìn chưa bao giờ cũ về thị trường C

Thị trường tài chính là nơi con người, tâm lý và dữ liệu va vào nhau. Mỗi chu kỳ lại tạo ra những người thắng lớn, và để lại bài học cho những người đến sau. Nếu nhìn lại hơn 100 năm lịch sử, có một nhóm nhỏ trader đã để lại dấu ấn đến mức dù bạn đang làm trading định lượng, discretionary hay macro thì triết lý của họ vẫn còn nguyên giá trị. Dưới đây là 10 trader mà bất kỳ ai nghiên cứu thị trường nghiêm túc cũng nên hiểu rõ. Không chỉ để ngưỡng mộ, mà để rút ra cách họ tư duy về rủi ro, xác suất, và tâm lý con người.

5 chiến lược thực tế để giảm thiểu rủi ro thị trường
13/10/2025
93 lượt đọc

5 chiến lược thực tế để giảm thiểu rủi ro thị trường C

Rủi ro thị trường (market risk) là rủi ro hệ thống ảnh hưởng đồng thời đến nhiều tài sản — không thể loại bỏ hoàn toàn nhưng có thể quản trị. Bài này trình bày phân tích chuyên sâu về bản chất các loại rủi ro thị trường, phương pháp đo lường chính, rồi đi vào 5 chiến lược giảm thiểu (risk tolerance, đa dạng hoá, hedging, giám sát liên tục, và tầm nhìn dài hạn). Cuối bài có phần cài đặt kỹ thuật và khuyến nghị quản trị.

Từ dữ liệu đến backtest: cách một chiến lược định lượng được hình thành
09/10/2025
75 lượt đọc

Từ dữ liệu đến backtest: cách một chiến lược định lượng được hình thành C

Nhiều người nghĩ rằng xây dựng một chiến lược định lượng chỉ đơn giản là kết hợp vài chỉ báo kỹ thuật, chạy backtest và chọn ra mô hình có đường equity “đẹp”. Nhưng thực tế thì khác xa — một chiến lược có thể tồn tại ngoài thị trường thật cần một quy trình rõ ràng, có kiểm định và giới hạn rủi ro ở từng bước.

video-image

Truy Cập Miễn Phí Thư Viện Bot Tín Hiệu Giao Dịch Tự Động

Được nghiên cứu và phát triển bởi các chuyên gia từ QMTrade và cộng đồng nhà đầu tư chuyên nghiệp.

Truy cập ngay!